TrajOpt [1] is an optimization based approach for motion planning. More specifically, it uses a sequential convex optimization procedure along with a formulation of collision constraints to find locally optimal planning trajectories, even for robotic systems that have a large number of degrees of freedom.
This post will go into the details of the optimization part, and give an outline of how it can be implemented. My implementation can be found here
$\newcommand{\R}{\mathbb{R}}$ $\newcommand{\Rn}{\mathbb{R}^n}$ $\newcommand{\Rm}{\mathbb{R}^n}$ $\newcommand{\Rnn}{\mathbb{R}^{n \times n}}$ $\newcommand{\Rmn}{\mathbb{R}^{m \times n}}$ $\newcommand{\half}{\frac{1}{2}}$ $\newcommand{\vline}{\Bigr|}$ $\newcommand{\st}{\text{s.t.}}$ $\newcommand{\x}{\mathrm{x}}$ $\newcommand{\e}{\mathrm{e}}$ $\newcommand{\nineq}{n_{ineq}}$ $\newcommand{\neq}{n_{eq}}$ $\newcommand{\Rnineqn}{\mathbb{R}^{\nineq \times n}}$ $\newcommand{\Rneqn}{\mathbb{R}^{\neq \times n}}$ $\newcommand{\Rnnnineq}{\mathbb{R}^{n \times n \times \nineq}}$ $\newcommand{\Rnnneq}{\mathbb{R}^{n \times n \times \neq}}$ $\newcommand{\xst}{{\mathrm{x}^\ast}}$ $\newcommand{\Tgixst}{\Omega_{g, i}(\xst)}$ $\newcommand{\Tgist}{{\Omega_{g, i}^\ast}}$ $\newcommand{\Thixst}{{\Omega_{h, i}(\xst)}}$ $\newcommand{\Thist}{{\Omega_{h, i}^\ast}}$ $\newcommand{\fx}{f(\x)}$ $\newcommand{\fc}{\tilde{f}}$ $\newcommand{\fcx}{\tilde{f}(\x)}$ $\newcommand{\gx}{g(\x)}$ $\newcommand{\gc}{\tilde{g}}$ $\newcommand{\gcst}{{\tilde{g}^\ast}}$ $\newcommand{\gcx}{\tilde{g}(\x)}$ $\newcommand{\gxi}{g_i(\x)}$ $\newcommand{\gci}{\tilde{g}_i}$ $\newcommand{\gcxi}{\tilde{g}_i(\x)}$ $\newcommand{\hx}{h(\x)}$ $\newcommand{\hc}{\tilde{h}}$ $\newcommand{\hcst}{{\tilde{h}^\ast}}$ $\newcommand{\hcx}{\tilde{h}(\x)}$ $\newcommand{\hxi}{h_i(\x)}$ $\newcommand{\hci}{\tilde{h}_i}$ $\newcommand{\hcxi}{\tilde{h}_i(\x)}$ $\newcommand{\tp}{\tau^{+}}$ $\newcommand{\tm}{\tau^{-}}$ $\newcommand{\wfxst}{\omega_f(\xst)}$ $\newcommand{\wfst}{\omega_f^\ast}$ $\newcommand{\Wfxst}{W_f(\xst)}$ $\newcommand{\Wfst}{{W_f^\ast}}$ $\newcommand{\Wgxst}{W_g(\xst)}$ $\newcommand{\Wgst}{{W_g^\ast}}$ $\newcommand{\Whxst}{W_h(\xst)}$ $\newcommand{\Whst}{{W_h^\ast}}$ $\newcommand{\Tgxst}{\Omega_g(\xst)}$ $\newcommand{\Tgst}{{\Omega_g^\ast}}$ $\newcommand{\Thxst}{{\Omega_h(\xst)}}$ $\newcommand{\Thst}{{\Omega_h^\ast}}$ $\newcommand{\tg}{t_g}$ $\newcommand{\sh}{s_h}$ $\newcommand{\th}{t_h}$ $\newcommand{\Dx}{\Delta \x}$
Theory
Motion planning problems can usually be fully represented as a non-linear, non-convex optimization problem of the form:
\begin{equation} \begin{aligned} \min f(\x)\\ \st \quad g_i(\x) \le 0, \ \ i = 1, 2, \ldots , \nineq\\ h_i(\x) = 0, \quad i = 1, 2, \ldots , \nineq\\ \end{aligned} \end{equation}
$f$, $g_i$ and $h_i$ are scalar non-convex functions with $\x \in \Rn$ being the vector of variables to optimize. For trajectory optimization algorithms, $\x$ consists of the sequence of control inputs and/or sequence of states (depending on the method used – direct, indirect, etc.) that can then be optimized to find the optimal robot trajectory.
Unfortunately, such optimization problems are usually NP-hard and we’re almost never guaranteed to find the global optima. Coupled with the fact that for motion planning, we usually require these problems to be solved quickly, most methods to solve such problems tend to gravitate towards using local optimization methods. One such popular method is Sequential Convex Programming (SCP).
Sequential Convex Programming
The main idea here is to convexify the non-convex problem at the current iterate, and take steps towards the minima found at each convex optimization solution.
\begin{equation} \begin{aligned} \min \fcx \\ \st \quad \gcxi \le 0, \ \ i = 1, 2, \ldots , \nineq\\ \hcxi = 0, \ \ i = 1, 2, \ldots , \nineq\\ \end{aligned} \end{equation}
Here, $\fc$, $\gci$ and $\hci$ are the convexified functions at the current value of $\x$ (denoted by $\x^\ast$). The SCP procedure looks something like this:
for iteration = 1, 2, $\ldots$ do
$\quad$ $\fc$, $\gc$, $\hc$ = ConvexifyProblem($f$, $g$, $h$) around $\x^\ast$
$\quad$ $\x^\ast \leftarrow \text{argmin}_{\x} \fcx \ \st \ \gcx \le 0, \ \hcx = 0$
Fairly straightforward, but there is still something missing. When we convexify the problem, we make a local approximation of the (potentially highly) non-convex function. We rely on the fact that this local approximation is accurate enough and can help drive us to a minima upon repeating the procedure. But irrespective of what approximation method we use, as we move away from the current $\xst$ around which the functions are convexified, it will start deviating from true values of the function.
What this means is that when we find the $\xst$ that minimizes a particular convexified problem, the actual value of $\x$ that minimizes the problem could be far away from $\xst$. This can lead to the algorithm getting to an updated value of $\x$ that is optimal according to the current convexified problem, but is not optimal according to the true non-convex problem.
To avoid this, SCP methods usually employ an additional trust region constraint, where we restrict the optimal value of $\x$ for a convexified step to be within a certain distance of $\xst$. The distance metric is some sort of norm (usually the $l^2$-norm) in most cases. If we define the trust region size as $s$, we now get:
for iteration = 1, 2, $\ldots$ do
$\quad$ $\fc$, $\gc$, $\hc$ = ConvexifyProblem($f$, $g$, $h$) around $\x^\ast$
$\quad$ $\x^\ast \leftarrow \text{argmin}_{\x} \fcx \ \st \ \gcx \le 0, \ \hcx = 0, \ \lVert \x - \x^\ast \rVert_2 \le s$
Instead of the $l^2$ ball constraint, we could also use an ellipsoidal constraint of the form $(\x - \x^\ast)^TP(\x - \x^\ast) \le s$ where $P \succ 0$.
Dynamic Trust Region Size
One strategy is to keep the trust region size small and fixed. This would guarantee that we’d be able to solve any convexified step and reliably get to some sort of local minima. But there are merits to using larger values of trust region size as well.
Consider a convexified step, where the convexified functions are almost an exact representation of the actual non-convex functions. In such a scenario, we could potentially take a large step while minimizing $\x$. Let’s say that in this situation a trust region size of $s = 1$ can get us to a new value of $\x$ that also minimizes the original non-convex problem. Compared to us using a smaller $s$ (Like around $1\e{-2}$, $1\e{-3}$), we could get to a similar $\x$ with much fewer iterations.
Dynamically varying the trust region size helps us get the best of both worlds. We can start with using a small trust region size and can progressively increase the size depending on how confident we are with the current convexified approximation. If we think that the convexified approximation is an accurate representation of the original problem around a larger region of $\x$, we can increase the trust region size and vice versa.
How do we know if the current problem approximation is a good one? We can use the new optimized value of $\x$ from the convexified problem and check how much it improves the original cost function as compared to the convexified cost function.
TrueImprove = $f(\x) - f(\xst)$
ModelImprove = $\fcx - \fc(\xst)$
As we’re minimizing the cost function, we expect the cost at the newly minimized value at $\xst$ to be lower, and so the difference tells us how much of an improvement there is.
As we’re minimizing the convexified cost function, it is a given that ModelImprove >= TrueImprove, but by computing the ratio of these terms, we can get an estimate of how much the original cost function improves upon solving the convexified problem.
IsImprovement
$\quad$ TrueImprove = $f(\x) - f(\xst)$
$\quad$ ModelImprove = $\fcx - \fc(\xst)$
$\quad$ return TrueImprove/ModelImprove > c
Let’s consider two extreme cases:
- The convexified problem is an exact representation of the non-convex problem (Maybe the original problem was even convex). In this case, $\xst$ will improve the original problem by the same amount as it improves the convexified problem. The ratio is 1 in this case.
- The convexified problem is an extremely poor representation of the non-convex problem. In this case $\xst$ will not improve the original problem by nearly as much. The ratio is close to 0 in this case.
We define some $c \le 1$ (Referred to as step acceptance parameter in the paper) and make an assumption that if the ratio is $> c$, the approximation is good and we can increase the trust region size. If not, we decrease the trust region size and don’t use the new $\xst$.
This now brings us to something similar to the trust region loop defined in the paper (more details on this later):
TrustRegionLoop
for TrustRegionIteration = 1, 2, $\ldots$ do
$\quad$ $\x^\ast \leftarrow \text{argmin}_{\x} \fcx \ \st \ \gcx \le 0, \ \hcx = 0, \ \lVert \x - \x^\ast \rVert_2 \le s$
$\quad$ if IsImprovement then
$\qquad$ $s \leftarrow \tp \ast s$
$\qquad$ break
$\quad$ else
$\qquad$ $s \leftarrow \tm \ast s$
$\quad$ if $s < xtol$ then
$\qquad$ break
Where we define $\tp \ge 1$ and $\tm \le 1$ as trust region expansion and shrinkage factors that decide how much the trust region expands or shrinks at each step.
If the trust region becomes too small, the problem will be numerically be stationary at a certain point. $xtol$ defines this smallest trust region size beyond which we break out of the loop. It also serves as the convergence threshold which we will get to next.
Convergence
The SCP also requires some criteria to stop the trust region loop. Usually this is defined as some threshold between the successive solutions of $\x$. Usually when we’re at a local/global minima, the gradients are zero and differences between successive solutions are minimal.
Depending on the function, we could also end up in a situation where a region around the minima corresponds to the same or similar cost values. So it’s generally a good idea to also have a convergence criteria on the value of the cost function as usually these would also stop moving much when we’re at a minima.
IsConverged
$\quad$ return $\lVert \xst - \x \rVert_2 < xtol$ or $\lVert f(\xst) - f(\x) \rVert_2 < ftol$
Where $xtol$ and $ftol$ are the corresponding convergence thresholds.
Constraints
Something that still needs to be addressed is the fact that we have non-convex constraints in the original problem. Solving the convexified problem with convexified constraints can still be tricky.
In the paper, these are added into the cost function as penalties rather than as constraints to the problem directly. Doing it this way simplifies things a lot as we can restrict the actual constraints to being linear and have the other terms as penalties in the cost function. We’ll go over this in detail in the implementation section, so for now we focus on how the penalties are formulated.
Consider the non-convex inequality constraints of the form $\gxi \le 0$.
In order to add this as a penalty in the cost function, we need to map it to a function that has a minimum at $0$ whenever the constraints are satisfied, and is positive everywhere else.
The paper uses $|\gxi|^+$ Where
\begin{equation}
|\gxi|^+ = \max(\x, 0)
\end{equation}
Whenever the constraints are satisfied, $\gxi \le 0$ which means that $|\gxi|^+ = 0$. So if we multiply this term by an extremely large penalty factor and add it to the cost function, it would force this term to go to zero (and hence satisfy the constraints) when the problem is solved. The minimizer of the penalized problem would be equal to the minimizer of the original problem with constraints.
Similarly for the non-convex equality functions $\hxi = 0$, we have a similar penalty function: \begin{equation} |\hxi| \end{equation}
Where $|\hxi|$ is just the absolute value of $\hxi$. Similar to the inequality function, this penalty function also has a minima at $0$ when the constraints are satisfied and is positive everywhere else. These constraints can also be multiplied by a penalty factor and incorporated into the cost function.
The cost function of the convexified problem which initially was
\begin{equation} \begin{aligned} \min \fcx \\ \st \quad \gcxi \le 0, \ \ i = 1, 2, \ldots , \nineq\\ \hcxi = 0, \ \ i = 1, 2, \ldots , \nineq\\ \end{aligned} \end{equation}
Now has a more numerically tractable form:
\begin{equation} \begin{aligned} \min \fcx + \mu \sum_i^{\nineq} |\gcxi|^+ + \mu\sum_i^{\neq}|\hcxi|\\ \st \quad \lVert \x - \xst \rVert_2 \le s\\ \end{aligned} \end{equation}
Given the current trust region size $s$ and the penalty factor $\mu$. Larger the value of $\mu$, the more likely it is for the optimization to prioritize satisfying the constraints over minimizing the pure cost $\fx$. When $\mu$ is very large (theoretically close to $\infty$), solving the problem would attempt to satisfy the constraints at any cost.
In order to check if the given constraints are satisfied, we have another procedure using a constraint satisfaction threshold $ctol$ (Where $0 < ctol \ll 1$). The threshold helps us relax the satisfaction requirements a bit when we actually implement it numerically. The check in practice becomes $\gxi \le ctol$ and $\lVert \hxi \rVert_2 \le ctol$
AreConstraintsSatisfied
$\quad$ for $i=1, 2, \ldots, \nineq$
$\qquad$ if $\gxi > ctol$ then
$\qquad$ $\quad$ return False
$\quad$ for $i=1, 2, \ldots, \neq$
$\qquad$ if $|\hxi| > ctol$ then
$\qquad$ $\quad$ return False
$\quad$ return True
It is important to note that the actual versions of the constraint functions are used here, and not the convexified versions.
Putting It All Together
Finally, we can take a look at how the paper integrates the penalty check, convexification and trust region loops.
-
The first step is to convexify the problem at the given $\xst$ and start the SCP trust region loop.
-
Depending on whether the new solution to the convexified problem is considered an improvement to the original cost function or not, we dynamically expand or shrink the trust region size. Ideally we continue this process until convergence, but what exactly do we need to do post trust region size modification?
-
Expansion: When the $\x$ minimizer solution is accepted, we want to increase the trust region size and re-convexify the problem at the new $\xst$. We would keep the new expanded trust region size and continue the SCP process.
-
Shrinkage: When the solution is not accepted, the trust region size is reduced and we don’t update $\xst$. There’s no need to convexify the problem as $\x$ hasn’t changed so we can reduce the trust region and try solving the convexified problem again. We keep repeating this until:
- The trust region size $s < xtol$ after which we need to break out of the loop and check for constraint satisfaction
- We reach the convergence criteria and we break out of the loop
All in all, we repeat the loop for a convexified version of the problem until a solution is accepted or the trust region becomes too small. Once we have a new solution, the problem is convexified again and the process is repeated.
-
-
Where do the penalties fit into all this? The convergence check only ensures that we have found a local optima for the current convexified version of the problem. It does not imply that $\xst$ satisfies the required constraints due to the nature of how the constraints are treated as cost function penalties. After each SCP iteration has converged, we check if the constraints are satisfied. There are only two scenarios:
- Satisfied: If the SCP has converged and the constraints are satisfied, we have satisfied the requirements of the problem. We have minimized the object (To the best of our numerical abilities, around a local convex estimate) and we have satisfied the required constraints. We can return the solution $\xst$ as the final minimizer of the optimization problem.
- Unsatisfied: If the SCP has converged and the constraints are not satisfied, we obviously need to start over, but what do we do differently? This is where the penalty factor comes into play. In this case, we can increase the penalty factor $\mu$ by some $k > 1$ by setting $\mu \leftarrow k \ast \mu$. We don’t have to start over from the initial value of $\x$ as the last SCP iteration converged and the only issues are the constraints not being satisfied. We can resume the SCP using the last updated values of $\xst$ and $s$, but with the new penalty factor $\mu$.
The entire algorithm now looks something like:
for PenaltyIteration = 1, 2, $\ldots$ do
$\quad$ for ConvexifyIteration = 1, 2, $\ldots$ do
$\qquad$ $\fc$, $\gc$, $\hc$ = ConvexifyProblem($f$, $g$, $h$)
$\qquad$ execute TrustRegionLoop
$\qquad$ if IsConverged then
$\qquad$ $\quad$ break
$\quad$ if AreConstraintsSatisfied then
$\qquad$ return $\xst$
$\quad$ else
$\qquad$ $\mu \leftarrow k \ast \mu$
Implementation
Now we get to the fun part of implementing it. In this section, we’ll go over how all of this can be implemented, along with some details that were skipped in the paper. For reference, my python implementation of the algorithm can be found here.
Convexifying The Cost
How do we actually go about convexifying the problem? In the paper, each of the functions are expanded about the current value of $\x$ using the Taylor series (Up until the second order). After doing this for each function, we can convert the non-convex optimization problem in to a Quadratic Program (QP) at each step.
More specifically, we can try to cast the problem into this specific form of the QP:
\begin{equation} \begin{aligned} \min \half x^TPx + q^Tx\\ \st \quad l \le Ax \le u\\ \quad x \in \Rn\\ \quad P \in \Rnn, q \in \Rn, A \in \Rmn\\ \quad l \in \Rm, u \in \Rm\\ \end{aligned} \end{equation}
Why this form in particular? Because this is a pretty standard form and also is the form of the inputs to OSQP, an open source and widely used optimization library for solving convex quadratic programs.
Expanding the cost function $\fx$ around $\xst$ up until the second order, we get
\begin{equation} \begin{aligned} \fcx = f(\xst) + \frac{\partial f}{\partial \x}^T\vline_{\x=\xst}(\x - \xst) + \half (\x - \xst)^T \frac{\partial^2 f}{\partial \x^2}^T\vline_{\x = \xst}(\x - \xst) \end{aligned} \end{equation}
To simplify things, we represent:
- The gradient vector at $\xst$, $\frac{\partial f}{\partial \x}^T\vline_{\x=\xst}$ by $\wfxst \in \Rn$
- The Hessian matrix at $\xst$, $\frac{\partial^2 f}{\partial \x^2}^T\vline_{\x = \xst}$ by $\Wfxst \in \Rnn$
- The difference $(\x - \xst)$ by $\Dx$
The convexified approximation now looks like:
\begin{equation} \begin{aligned} \fcx = f(\xst) + \wfxst^T\Dx + \half \Dx^T \Wfxst \Dx \end{aligned} \end{equation}
To get it into the standard QP form, we need to expand $\Dx$ and separate out the first and second order terms of $\x$. After simplification, this gives us:
\begin{equation} \begin{aligned} \fcx = \half \x^T \Wfxst \x + (\wfxst - \half(\Wfxst + \Wfxst^T)\xst) ^T \x \end{aligned} \end{equation}
Note that we have dropped the terms that do not depend on $\x$ (Such as $f(\xst)$, $\xst^{T} \Wfxst \xst$ and $\wfxst^{T} \xst$) as they are constant with respect to the optimization variable.
As we can see the coefficients of the first order $\x$ terms will be incorporated in the $q$ matrix and the second order terms in the $P$ matrix of the final QP formulation.
Convexifying The Constraints
In a similar fashion, we can convexify the constraints. Like in the paper, we can think of it as individual scalar valued $\gxi$, $\hxi$ constraints, but I find it easier to work with vector valued constraints $\gx$ and $\hx$ where the outputs are a vector, each value corresponding to one constraint in $\x$.
In this case, as both the inputs and outputs of the functions are vectors, the gradients of the functions are matrices and the Hessians are tensors. We represent them evaluated at $\xst$ as $\Wgxst \in \Rnineqn$, $\Whxst \in \Rneqn$, $\Tgxst \in \Rnnnineq$ and $\Thxst \in \Rnnneq$ for the constraint function families $g$ and $h$. We can think of the tensors to be comprised of individual Hessian matrices $\Tgixst \in \Rnn$ and $\Thixst \in \Rnn$.
Similar to the cost function, we can convexify the constraint functions using the Taylor series expansion.
\begin{equation} \begin{aligned} \gcx = g(\xst) + \Wgxst\Dx + \half \Dx^T \sum_i^{\nineq}\Tgixst \Dx\\ \hcx = h(\xst) + \Whxst\Dx + \half \Dx^T \sum_i^{\neq}\Thixst \Dx\\ \end{aligned} \end{equation}
Incorporating The Constraints
We go back to an important bit in the paper. We still need to reformulate the penalties in a way that can passed off to a solver. If the $\gxi$ constraints can be linearized, the penalty function $|\gxi|^+$ can be written as $|a \cdot x + b|^+$. The problem of minimizing \begin{equation} \begin{aligned} \min |a\cdot x + b|^+ \end{aligned} \end{equation}
Can equivalently be written as
\begin{equation} \begin{aligned} \min \tg\\ \st \quad \tg \ge 0\\ a\cdot x + b \le \tg\\ \end{aligned} \end{equation}
In a similar vein, $\min |\hxi|$ can be written as $\min |a\cdot x + b|$. Upon the introduction of more slack variables, we get:
\begin{equation} \begin{aligned} \min \sh + \th\\ \st \quad \sh \ge 0\\ \st \quad \th \ge 0\\ \sh - \th = a\cdot x + b\\ \end{aligned} \end{equation}
But $\gcx$ and $\hcx$ have both quadratic and linear $\x$ terms. What do we do in this case?
Luckily the nature of the penalty functions makes it easy to separate them out.
\begin{equation} \begin{aligned} |\gci|^+ = |g(\xst) + \Wgxst\Dx + \half \Dx^T \sum_i^{\nineq}\Tgixst \Dx|^+\\ = \half \Dx^T \sum_i^{\nineq}\Tgixst \Dx + |g(\xst) + \Wgxst\Dx|^+\\ \end{aligned} \end{equation}
We can pull the quadratic term out as it will be $\ge 0$ if each $\Tgixst \succeq 0$. Positive semi-definitiveness of the Hessians is a reasonable assumption to make, and even if they aren’t, we can modify and deal with them numerically.
We also expand the quadratic term to separate out the quadratic and linear terms in $\x$. We get something similar to the cost function expansion.
\begin{equation} \begin{aligned} \half \x^T\sum_i^{\nineq}\Tgixst \x - \half \xst^T \sum_i^{\nineq} (\Tgixst + \Tgixst^T) \x + |g(\xst) + \Wgxst\Dx|^+ \end{aligned} \end{equation}
Similarly for the equality constraints:
\begin{equation} \begin{aligned} |\hci| = |h(\xst) + \Whxst\Dx + \half \Dx^T \sum_i^{\neq}\Thixst \Dx|\\ = \half \x^T\sum_i^{\neq}\Thixst \x - \half \xst^T \sum_i^{\neq} (\Thixst + \Thixst^T) \x + |h(\xst) + \Whxst\Dx| \end{aligned} \end{equation}
So now we have linear terms, which can be incorporated through the slack variables into the cost function, along with linear constraints in $\x$ and the slack variables themselves. What do we do about the quadratic term? Dropping them is a bad idea as then there would be nothing in the cost function to numerically push $\x$ to a region that satisfies constraints (The slack terms are there but they don’t perform this function). The only reason using the penalty factor $\mu$ works is that there is some term in the convexified constraint functions that push the entire cost around.
We can simply add the quadratic terms directly into the cost and incorporate them into the $P$ matrix.
Finally, we look at what the linear constraint terms look like.
\begin{equation} \begin{aligned} g(\xst) + \Wgxst\Dx\\ \end{aligned} \end{equation}
This is linear in $\Dx$ but we need them to be linear in $\x$. Similar to what we did for $f$, we can expand and separate out the terms. We then write out linear inequality in a way required by the QP. We have:
\begin{equation} \begin{aligned} g(\xst) + \Wgxst\Dx \le \tg\\ \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \Wgxst\x - \tg \le \Wgxst\xst - g(\xst)\\ \end{aligned} \end{equation}
For the non-convex equality constraints, we have:
\begin{equation} \begin{aligned} \Whxst\x - \sh + \th = \Whxst\xst - h(\xst)\\ \end{aligned} \end{equation}
Final QP
After convexifiying the functions, the QP can be written as:
\begin{equation} \begin{aligned} \min \half \x^T \Wfst \x + (\wfst - \half(\Wfst + \Wfst^T)\xst) ^T \x +\\ \mu(\half \x^T\sum_i^{\nineq}\Tgist \x - \half \xst^T \sum_i^{\nineq} (\Tgist + \Tgist^T) \x) + \mu(\half \x^T\sum_i^{\neq}\Thist \x - \half \xst^T \sum_i^{\neq} (\Thist + \Thist^T) \x) + \mu(\tg + \sh + \th)\\ \st \quad lb \le \x \le ub\\ \lVert \xst - \x \rVert_2 \le s\\ A_g\x \le b_g\\ A_h\x = b_h\\ \Wgst\x - \tg \le \Wgst\xst - \gcst\\ \Whst\x - \sh + \th = \Whst\xst - \hcst\\ \end{aligned} \end{equation}
We abuse the notation slightly, where $[ \ ]^\ast$ refers to a quantity measured at $\xst$.
Note that in addition to the constraints mentioned previously, we also have $lb \le \x \le ub$ constraints on the state as well as pure linear inequality and equality constraints (defined by
$(A_g, b_g)$ and $(A_h, b_h)$) for which we don’t require any slack terms.
One final thing to note is that the trust region constraints $\lVert \xst - \x \rVert_2 \le s$ is not linear which would make the problem a QCQP instead. There are a bunch of ways around this:
- Solve the problem as a QCQP using a compatible solver
- Expand the second order constraints in terms of its gradients and Hessians like the non-convex constraints and incorporate it that way. We don’t lose out on anything doing this because the norm constraint is convex in the first place
- Replace the $l^2$ norm constraints using box constraints of the form $\xst - s \le x \le \xst + s$. This is the easiest way around the problem and works pretty well in practice. This is what the paper employs for solving some of the higher DOF problems.
We can write the optimization problem in the standard QP form:
\begin{equation} \begin{aligned} \min \half z^TPz + q^Tz\\ \st \quad l \le Az \le u\\ \end{aligned} \end{equation}
Where $z$ is a variable that holds the original variables and the slack terms.
\begin{equation} \begin{aligned} z = \begin{bmatrix} \x^T, \tg^T, \sh^T, \th^T \end{bmatrix}^T \end{aligned} \end{equation}
The other quantities are:
\begin{equation} \begin{aligned} P = \Wfst + \mu \sum_i^{\nineq}\Tgist + \mu \sum_i^{\neq}\Thist \end{aligned} \end{equation}
\begin{equation} \begin{aligned} q = \begin{bmatrix} \wfst - \half(\Wfst + \Wfst^T)\xst + \mu\left(- \half \xst^T \sum_i^{\nineq} (\Tgist + \Tgist^T) - \half \xst^T \sum_i^{\neq} (\Thist + \Thist^T)\right) \\ \mu\\ \vdots\\ \mu\\ \end{bmatrix} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} A = \begin{bmatrix} I^{n \times n} & 0^{n \times ns}\\ I^{n \times n} & 0^{n \times ns}\\ A_g & 0^{n_{A_g} \times ns}\\ A_h & 0^{n_{A_h} \times ns}\\ \Wgst & \begin{bmatrix} -I^{\nineq \times \nineq} & 0^{\nineq \times 2\neq}\\ \end{bmatrix}\\ \Whst & \begin{bmatrix} 0^{\neq \times \nineq} & -I^{\neq \times \neq} & I^{\neq \times \neq}\\ \end{bmatrix} \end{bmatrix} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} l = \begin{bmatrix} lb\\ \xst - s\\ -\infty^{n_{A_g}}\\ b_h\\ -\infty^{\nineq}\\ \Whst\xst - \hcst\\ \end{bmatrix} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} u = \begin{bmatrix} ub\\ \xst + s\\ b_g\\ b_h\\ \Wgst\xst - \gcst\\ \Whst\xst - \hcst\\ \end{bmatrix} \end{aligned} \end{equation}
Libraries
My implementation uses OSQP to solve the QP at each SCP step. Most solvers and optimization libraries support quadratic programming, so this part is pretty straightforward.
For simple problem setups, we can manually compute the function derivatives, but for more complex setups this might not be an option. High DOF systems with large number of constraints will require the computation of large Hessian tensors which can be painstaking (and sometimes impossible) to compute analytically.
I’ve found JAX to be a godsend in these scenarios. It can compute the derivatives of any of your functions to your required degree (provided the function is actually differentiable that many times) and also comes with other useful features to speed up computation using GPU/parallel processing and just in time compilation. Convexifying functions becomes a breeze as you can compute gradient and hessian functions extremely easily.
import jax
def f(x: np.ndarray, ...) -> float:
...
grad_f = jax.grad(f)
hess_f = jax.hessian(f)
x = ...
grad_at_x = grad_f(x)
hess_at_x = hess_f(x)
The Not So Obvious Bits
Here’s a list of things that might not be obvious from a paper read through:
-
Linear constraints might feel warm and fuzzy, but can break the problem if we’re not careful. Consider the scenario where we’re optimizing for a scalar $\x$ with a constraint $\x \ge 100$. Let’s say that our initial guess of $\x$ is 0. Given the fact that our trust region is small initially, this would lead to an infeasible QP as the linear constraint is violated at the first iteration itself. There’s no way for the optimizer to deal with this due to the small trust region. This means that:
- We need to be careful about how we go about choosing the initial $\x$ in general
- Starting the problem off with linear constraints violated could be a recipe for disaster
We could do some numerical magic like introduce penalties and let the cost function drive $\x$ into the feasible space when this happens but it just complicates things unnecessarily. It’s best to leave the complicated bits to decades of optimization research that we have access through current day solvers. Most problems in robotics usually have linear constraints that can be navigated around easily (such as goal state constraints, etc.)
-
This one is more obvious, but we need to make sure to drop the solution when the cost function improvement ratio does not pass our acceptance threshold. Using the new $\xst$ in this case can lead to the problem being unable to find a way forward, even after reducing the trust region size as it might be impossible to backtrack from that position.
-
If the value of the constraint satisfaction threshold $ctol$ is not high enough, solvers will find it difficult to numerically converge to constraint satisfying solutions. Keeping it reasonably high will help in progressing the SCP at the correct times and will also speed up the overall solve time.
-
It might seem logical to keep a high penalty factor initially, but this can come at the cost of sub-optimal solutions. The factor can always scale up later on once the constraints don’t get satisfied.
-
I covered this earlier but to re-iterate, if we don’t include the quadratic terms of the convexified constraint functions in the overall cost function, there is nothing in the cost that will help drive the solution from infeasible to feasible regions.
-
We don’t really need to make a distinction for pure linear constraints and add them in as direct constraints without the slack terms. We could treat them as non-convex functions and follow the same procedure. The problem is equivalent and has the same optimum no matter which way we go about doing it. Not treating them as a special case makes the actual implementation a bit easier, but adding them directly should still be preferred as it reduces the overall program size by not having the additional slack terms.
Evaluation
We can now evaluate the algorithm on some examples. For this post, we’ll go over how it operates on the Rosenbrock function. Its application on some actual robotic systems will be covered in another post.
The Rosenbrock function is a non-convex function that is a nice test bed to test the performance of non-convex optimization methods. It isn’t difficult to solve for but helps us get a good understanding of what the algorithm is doing under the hood. It also helps with easier debugging when implementing such algorithms.
\begin{equation} \begin{aligned} f(x, y) = (a - x)^2 + b(y - x^2)^2 \end{aligned} \end{equation}
We test on the 2-dimensional version as this lets us visualize the algorithm and see what’s going on at each step. We use $(a=1, b=100)$, which makes the function have a global minimum at $(1, 1)$ with a value $f(x, y) = 0$
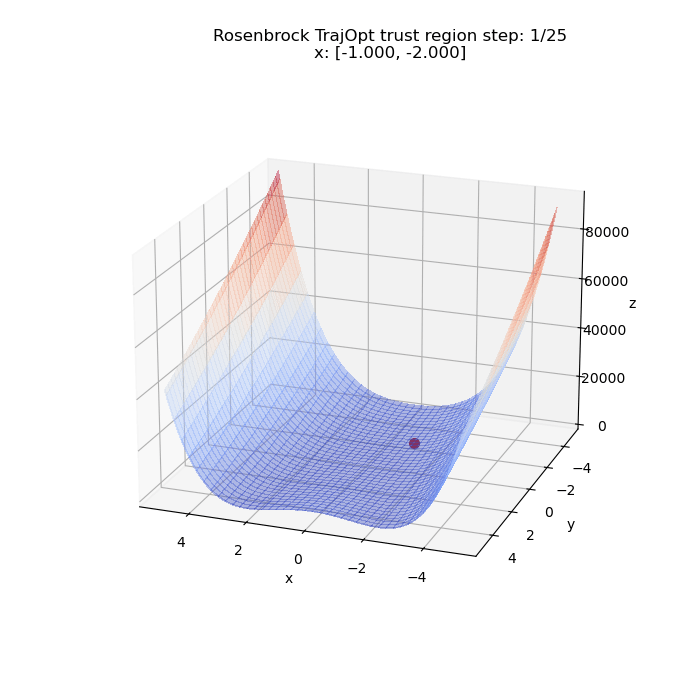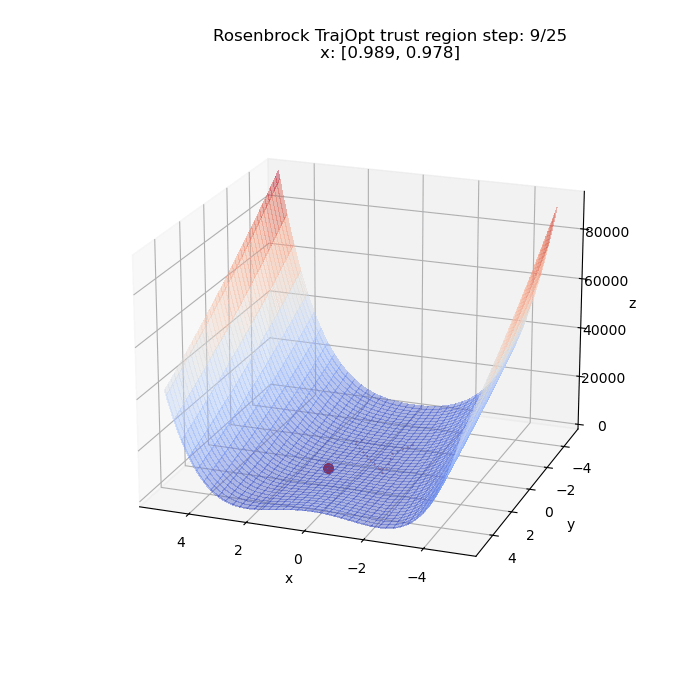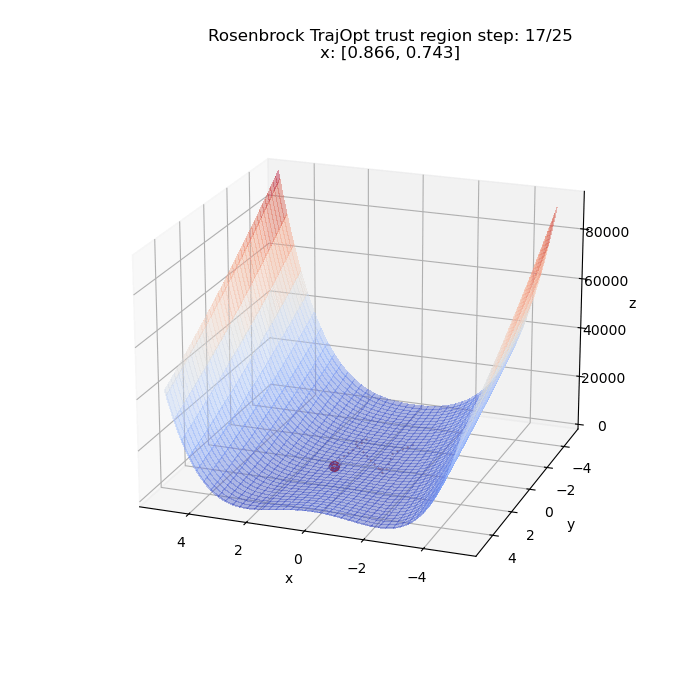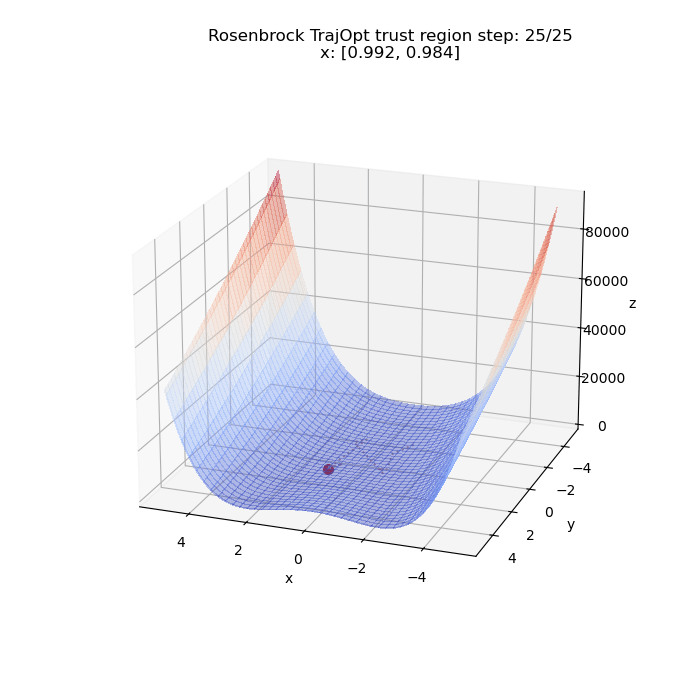
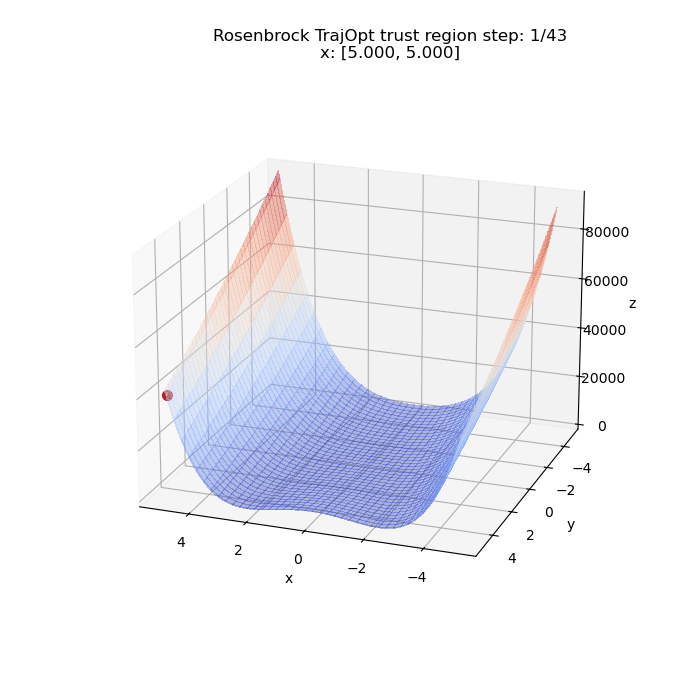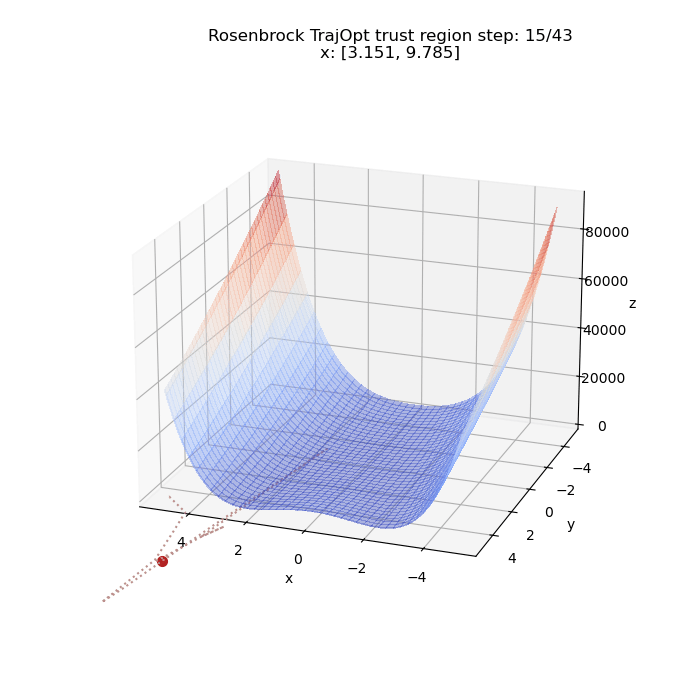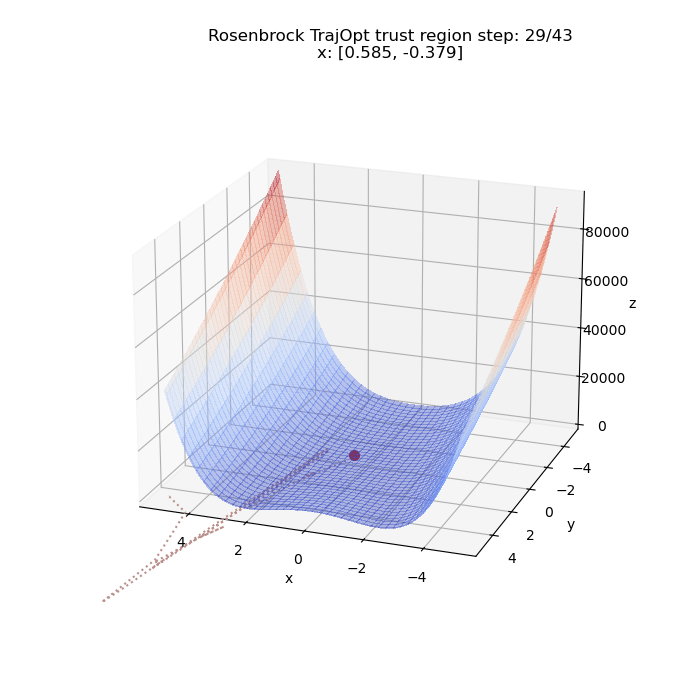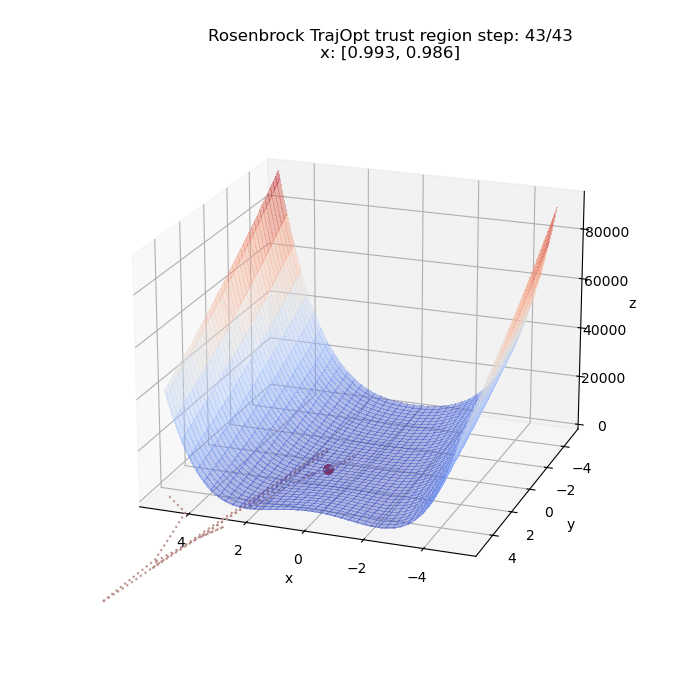
First, we try to minimize the problem unconstrained. Below we have a visualization of $\x = (x, y)$ from the initial to the final value as optimized by the algorithm. The initial value in this case is $(-1, -2)$. We can see it converge to the global minima at $(1, 1)$ (upto a tolerance) and the path it took to get there.
We can run the same thing for a different starting point. This time from $(5, 5)$
Time to start adding constraints!
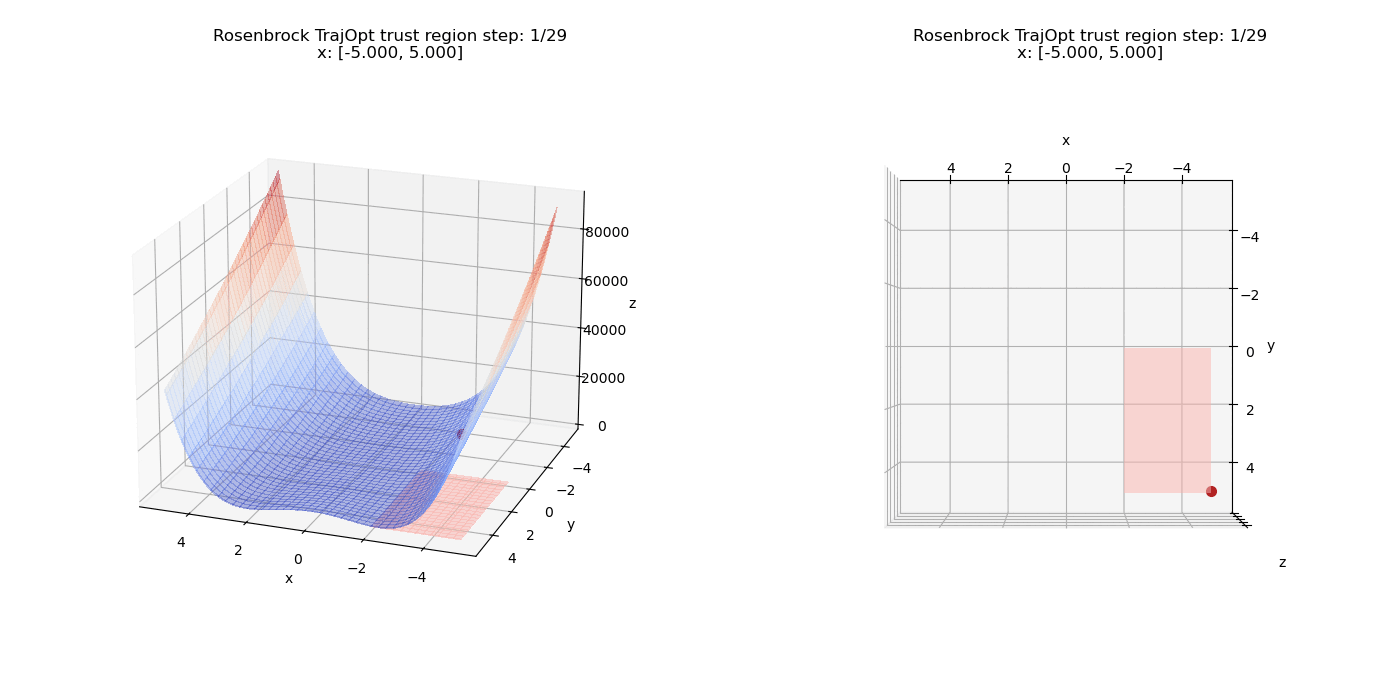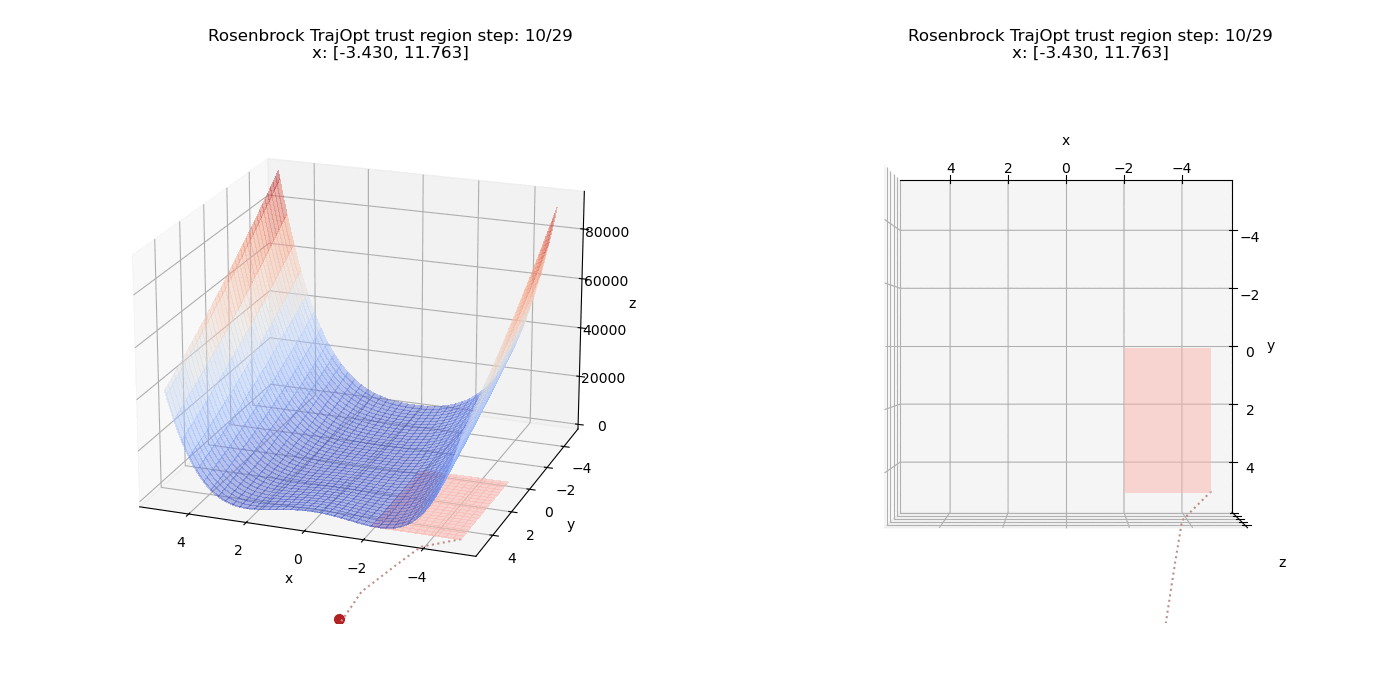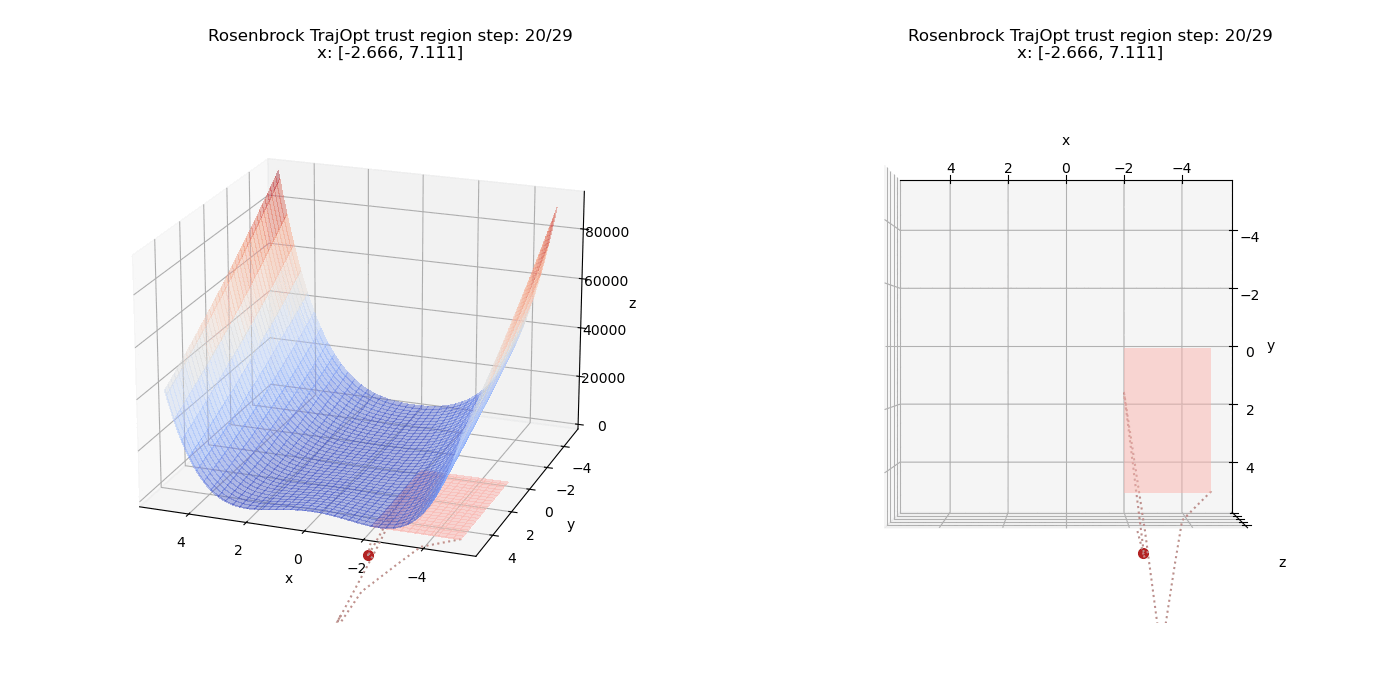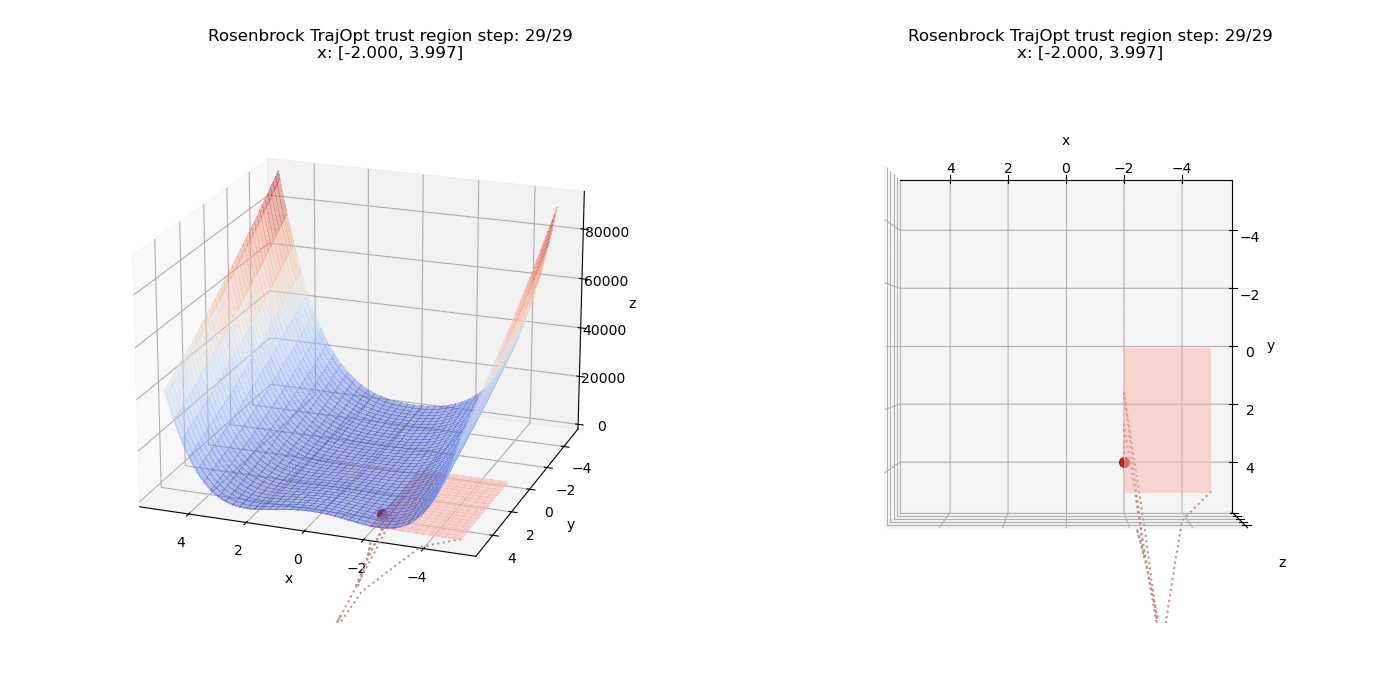
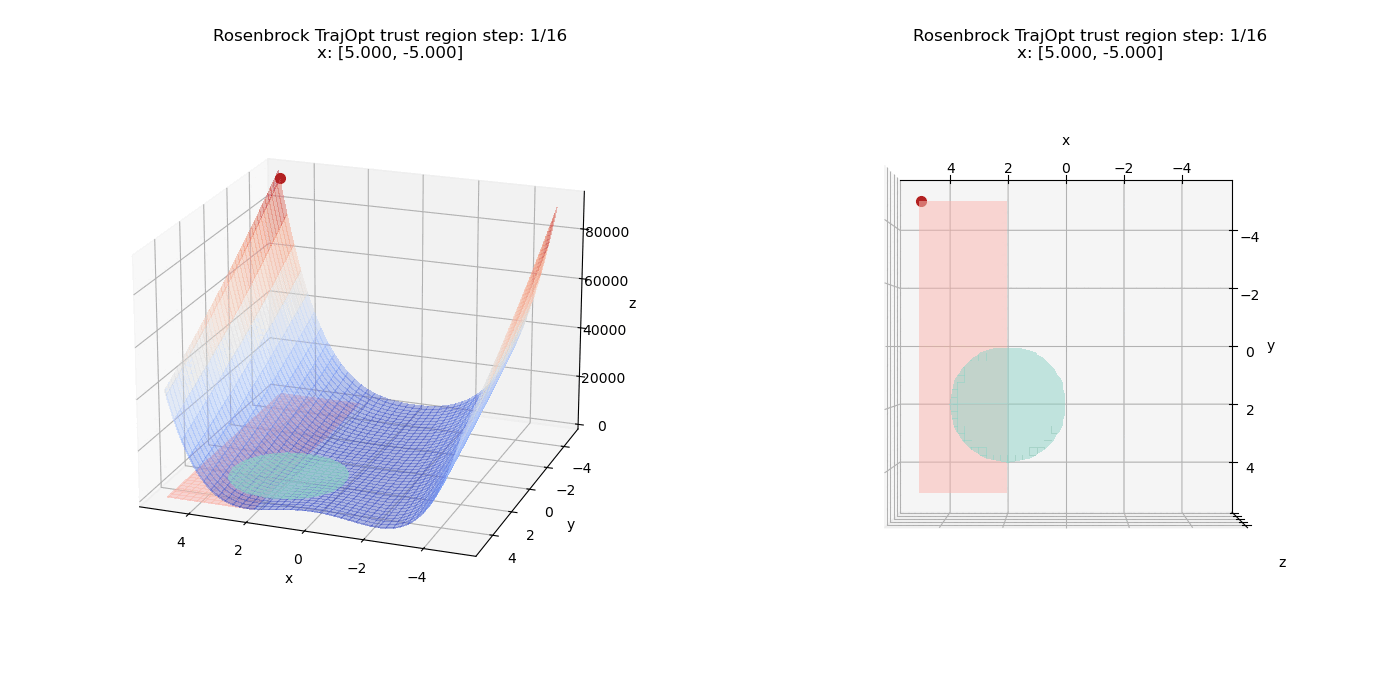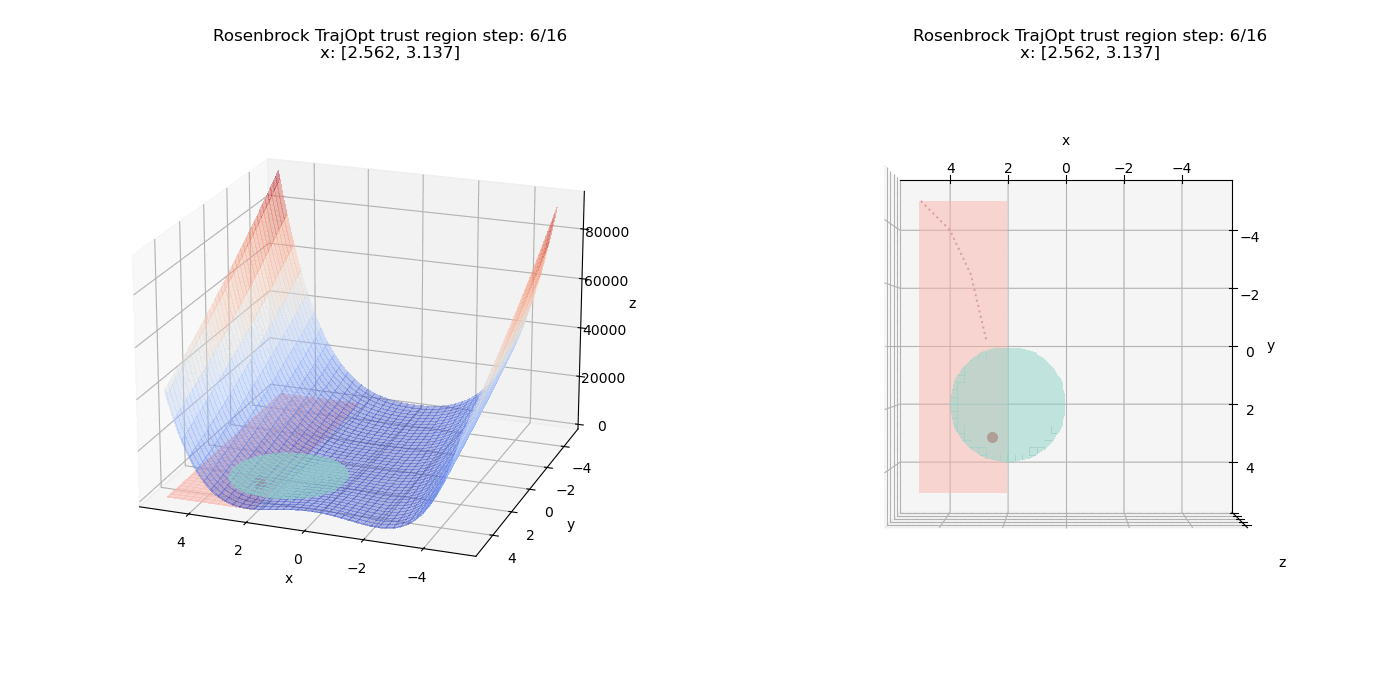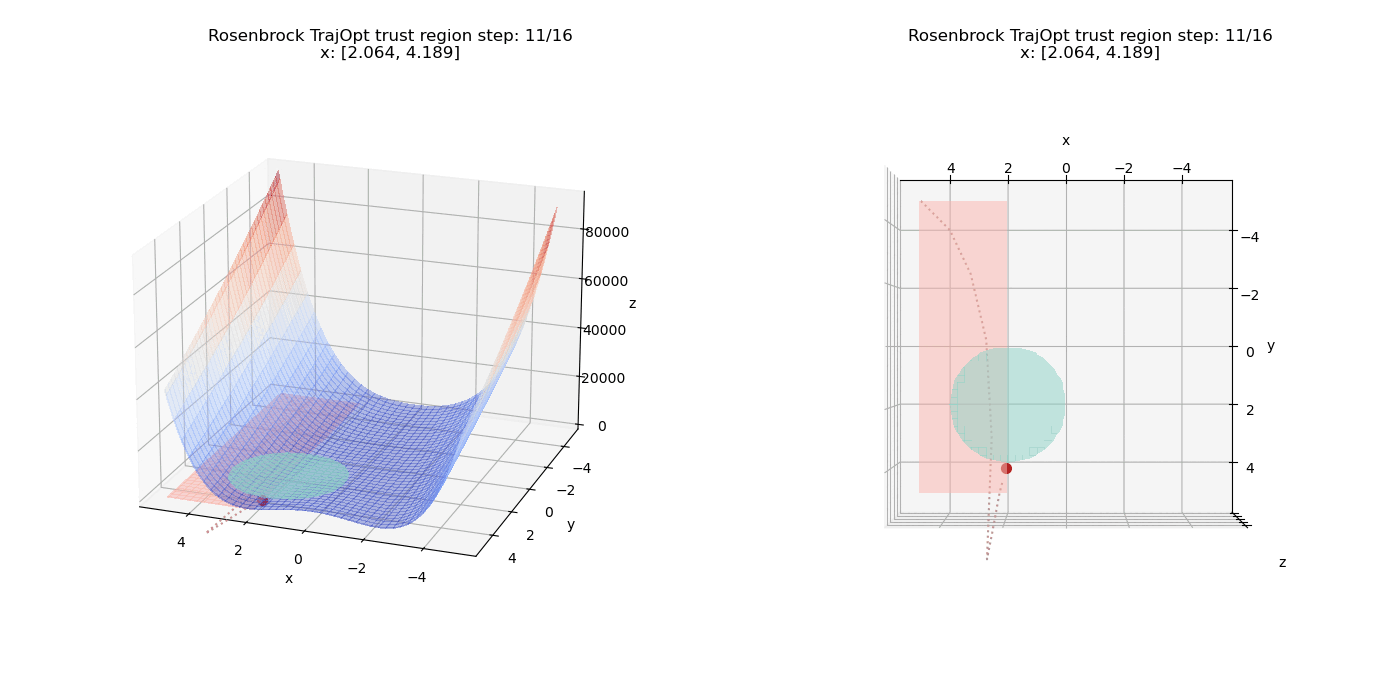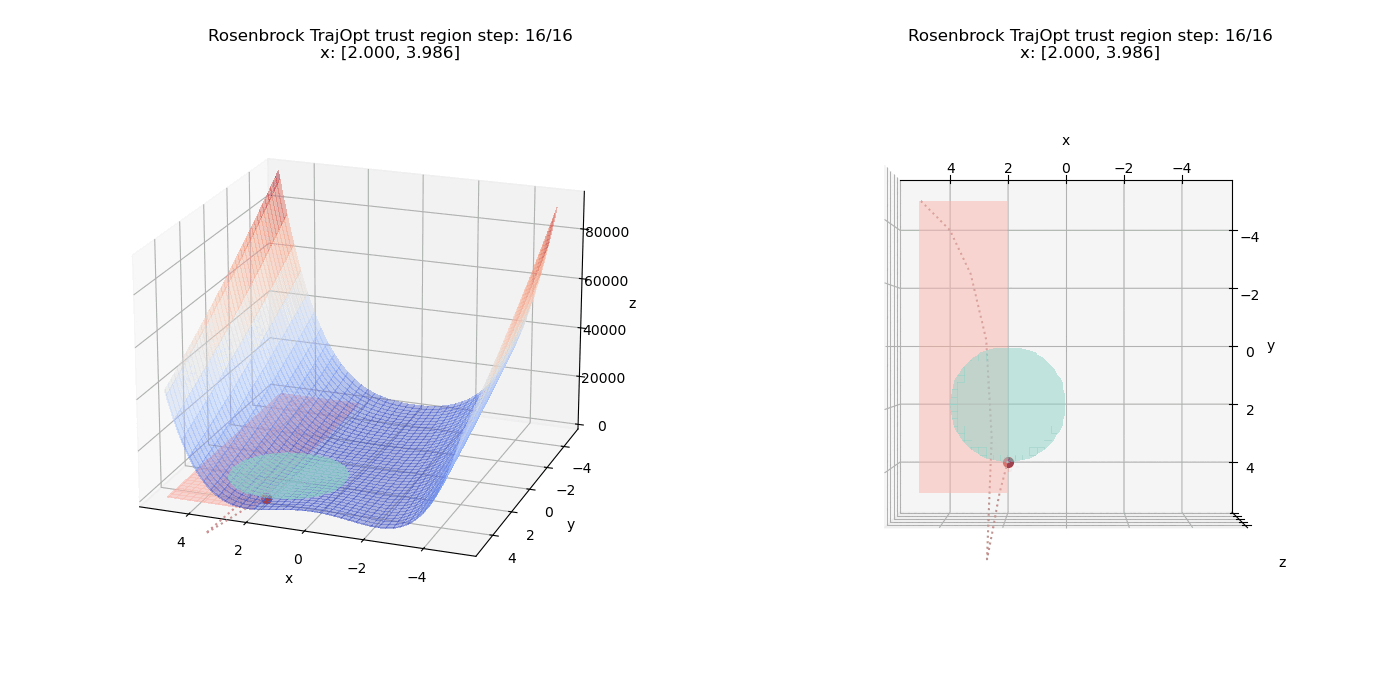
To start off, we add a pure linear constraints that specify $(x \le -2, y \ge 0)$. we can see how the point moves on the cost surface and the constraint feasibility region (shaded in pink).
Now we test non-linear constraints.
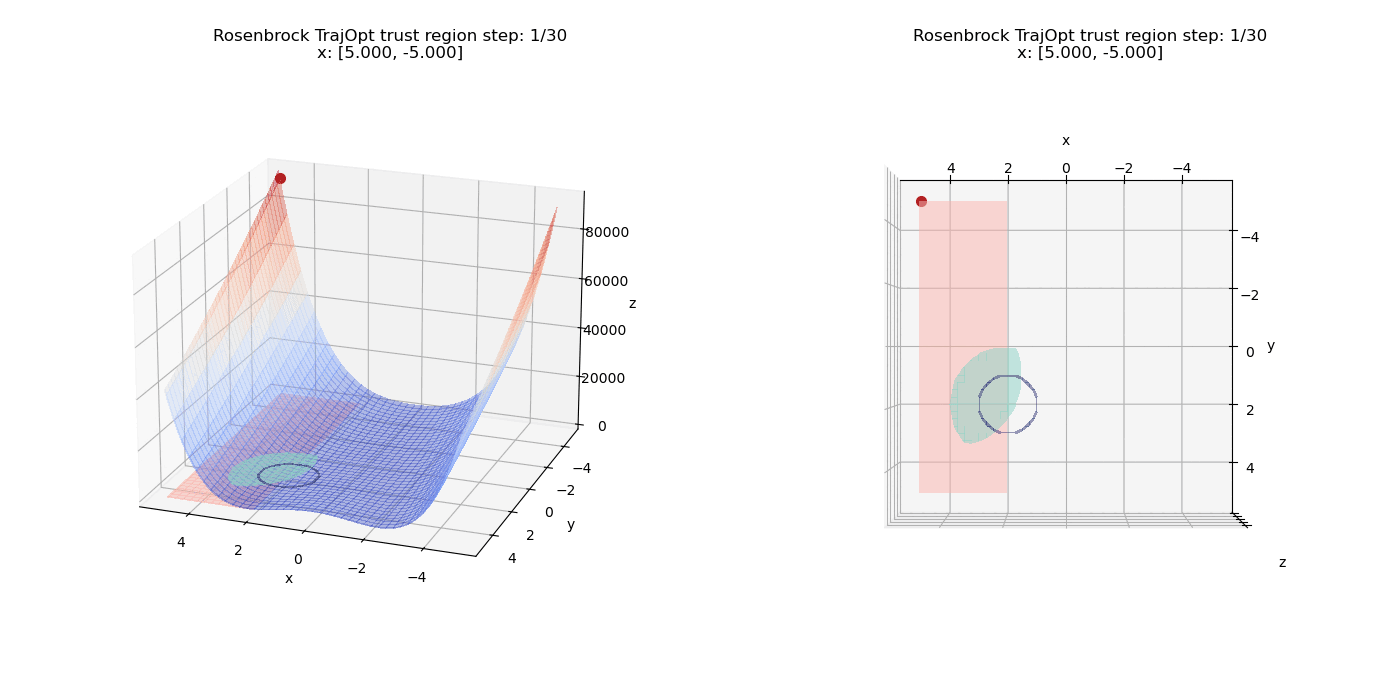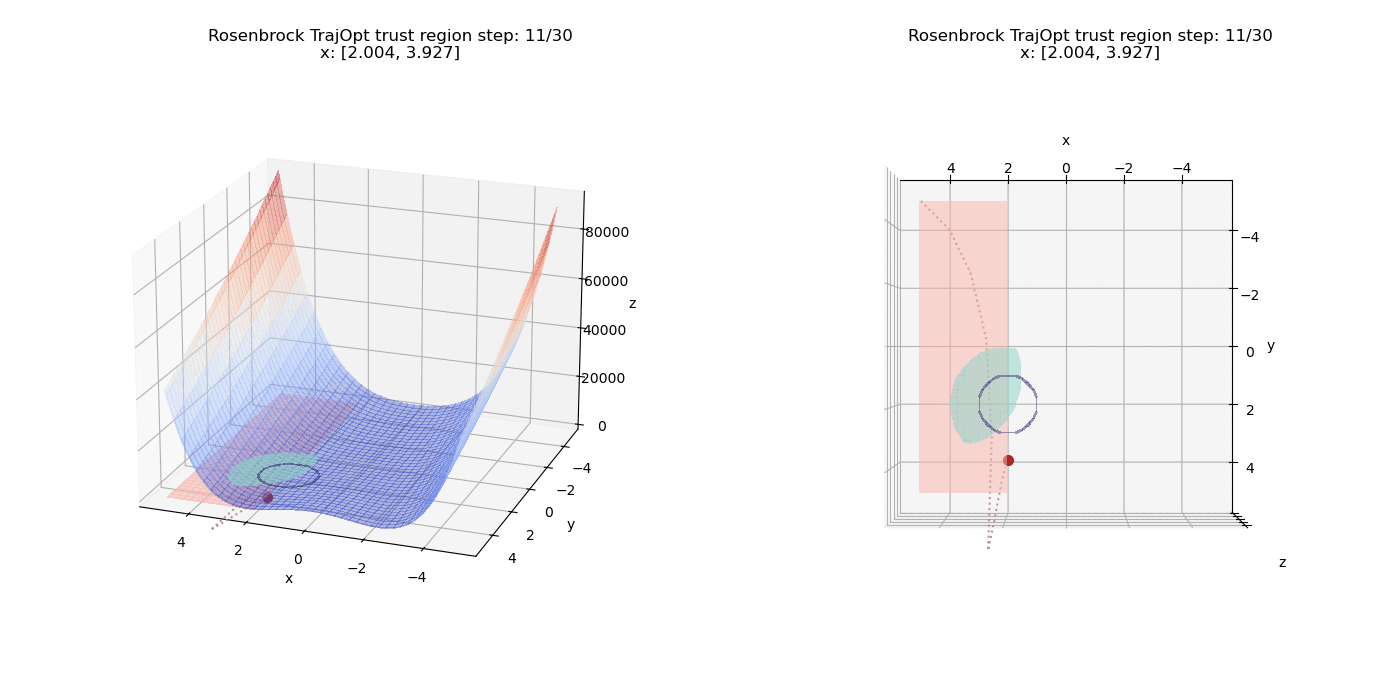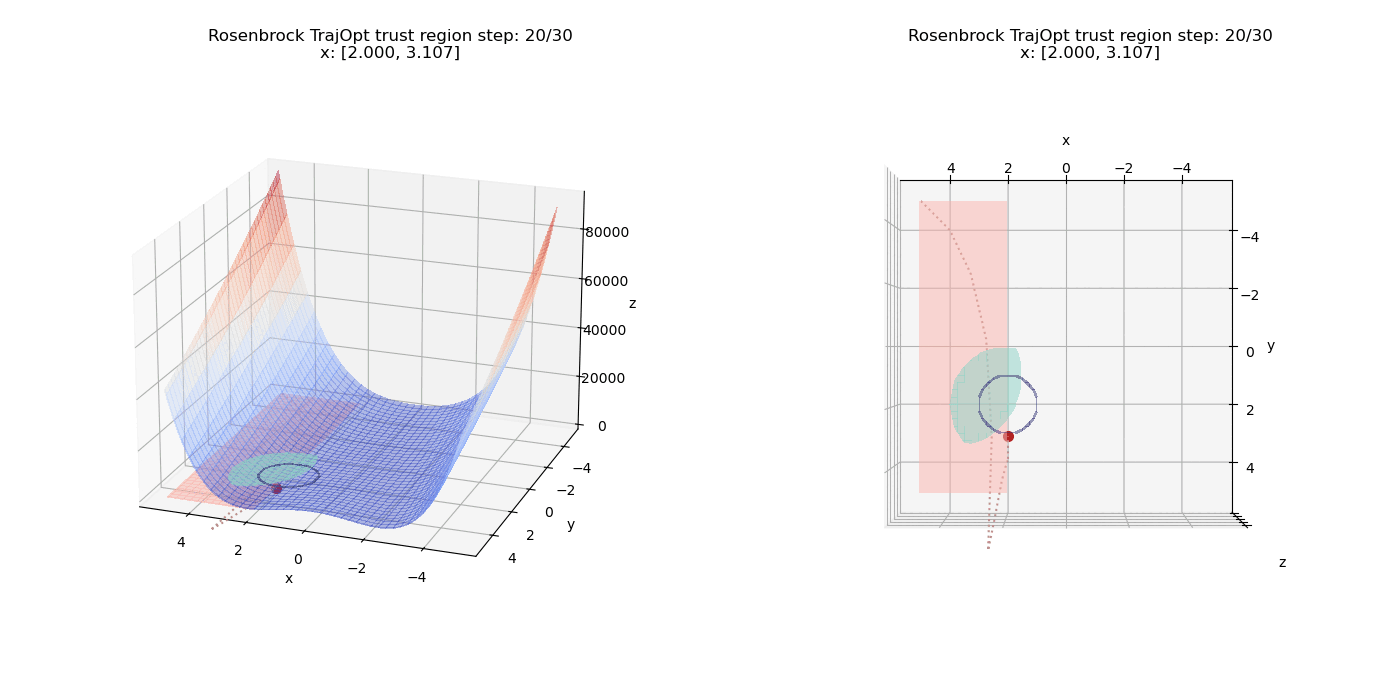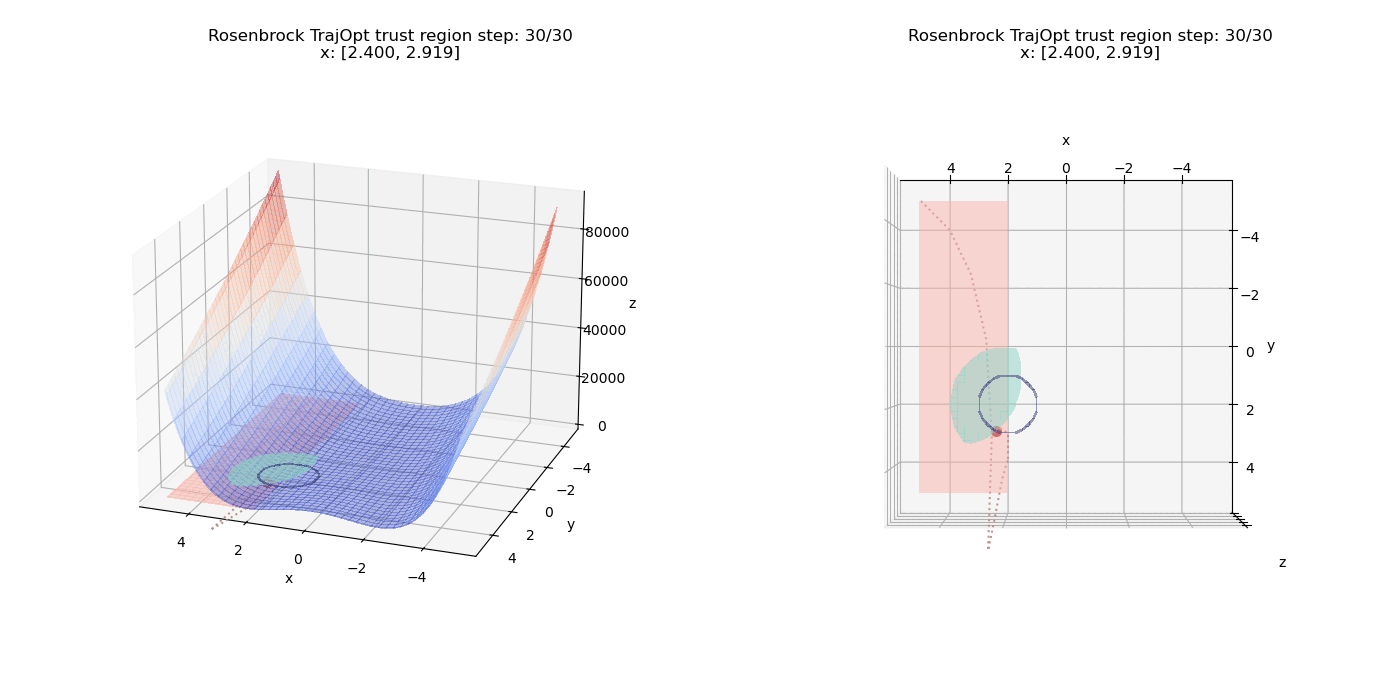
The linear constraints have been updated to $(x \ge 2, y \ge -5)$
We also have another constraint $(x - 2)^2 + (y - 2)^2 \le 4$ which defines a circular region in the X-Y plane (shaded in teal).
We can see how the point passes through and overshoots the circular region initially but the increased penalty factor drives the point back through the quadratic term of the constraint function.
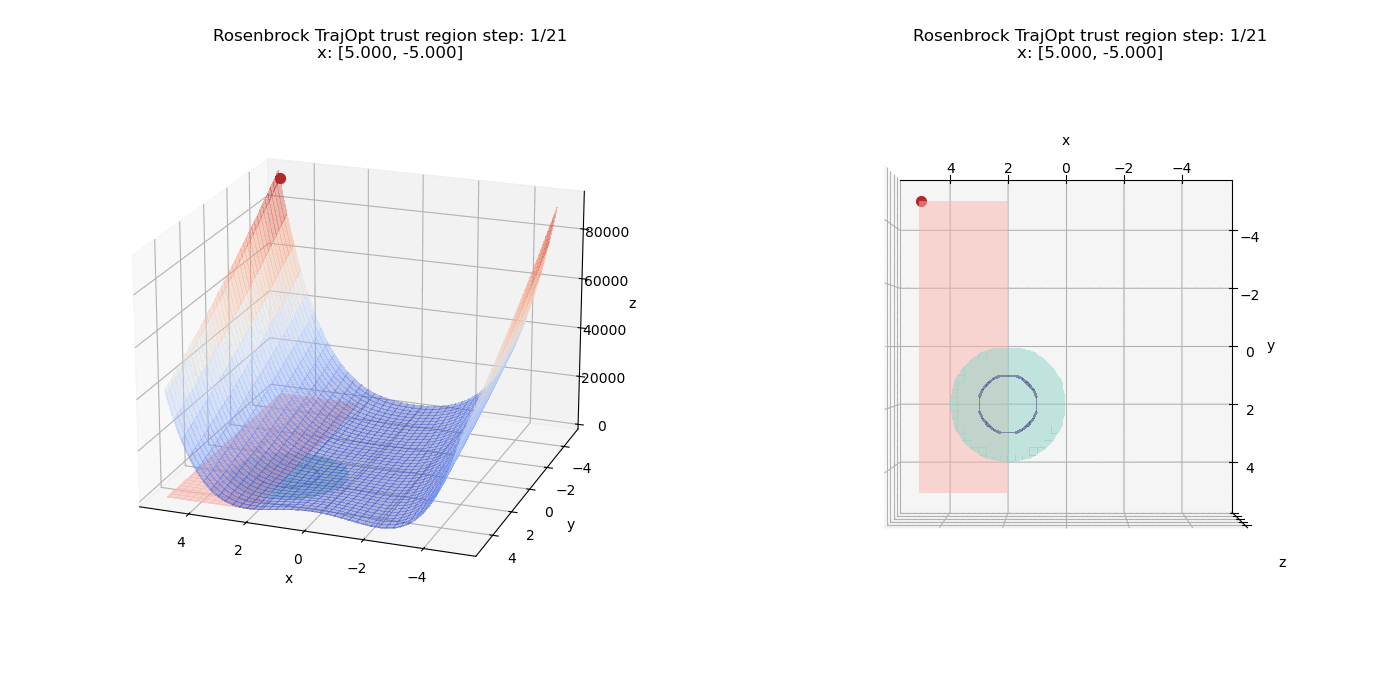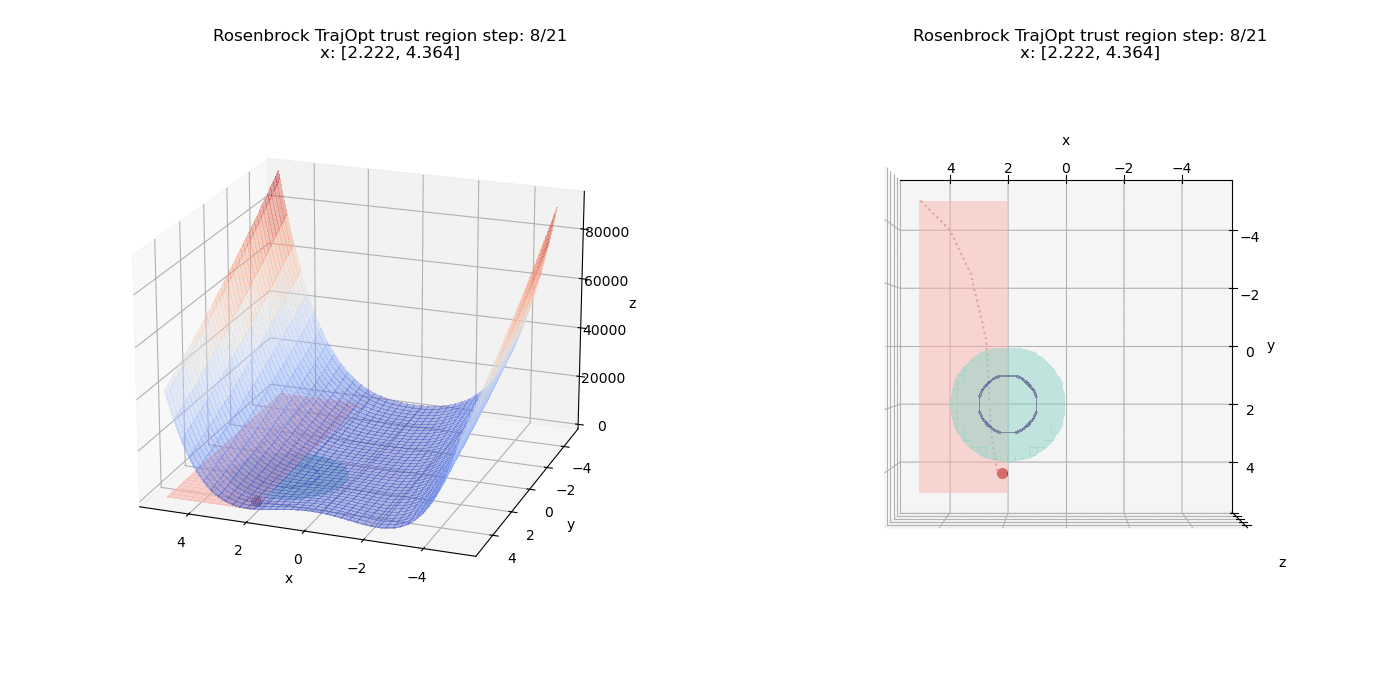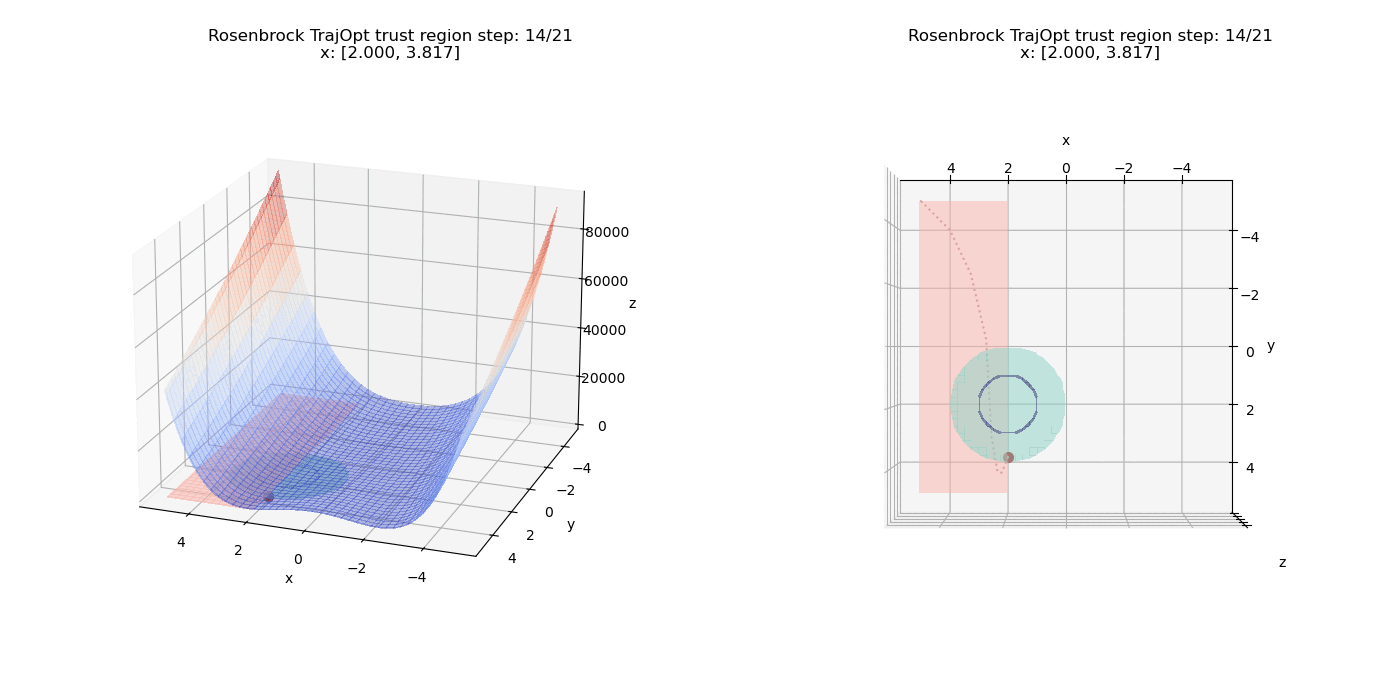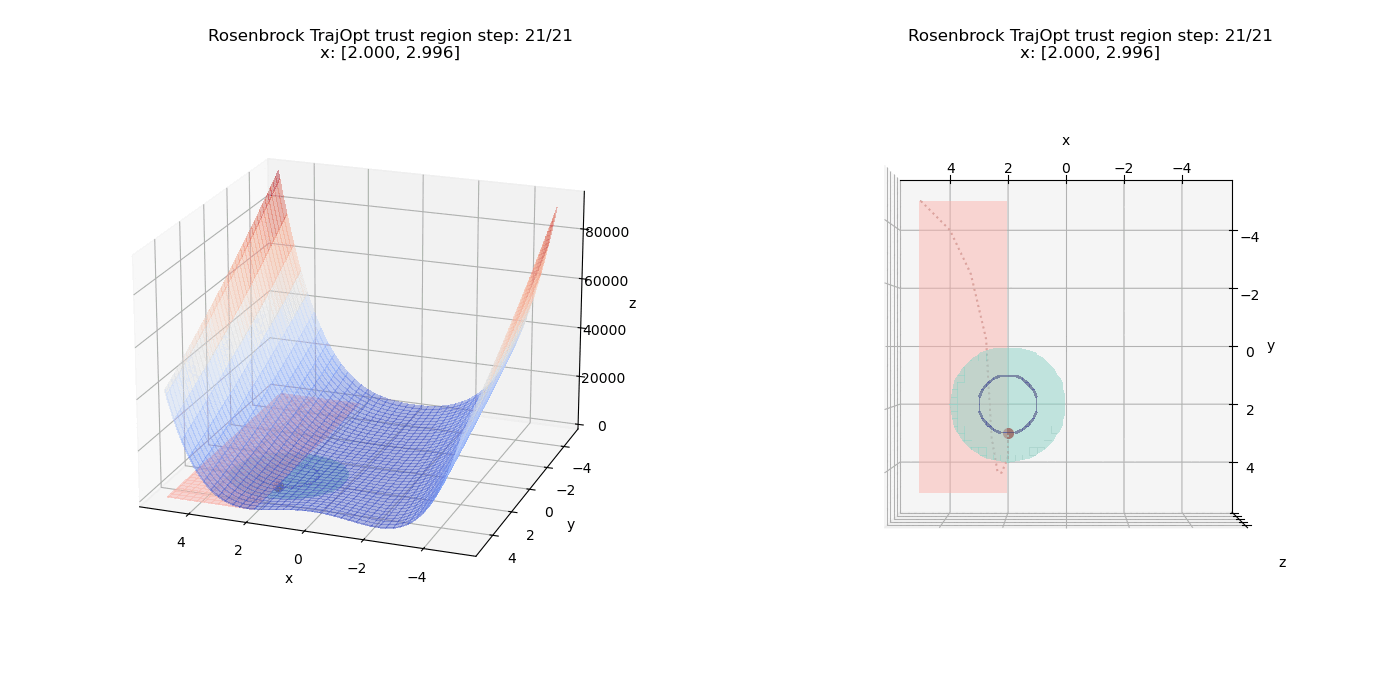
Now we add an equality constraint of the form $(x - 2)^2 + (y - 2)^2 = 1$ to the existing set of constraints. Note that this is a circle of half the radius of the inequality region and the constraint now requires the solution to lie exactly on this smaller circle and not just within the larger inequality region. So the final solution will need to lie well within the inequality constraint region and not just at the surface like the previous setup. The equality region is the dark blue colored ring as seen below:
Again we can see the costs balancing out and the equality constraint pushing the point further into the circular region (Once $\mu$ gets large enough) until it satisfies the equality constraint.
To top things off, we introduce another inequality constraint $(x - 4)^2 + (y - 1)^2 \le 6.25$ along with all the other constraints. The feasible inequality region is the intersection of both the circular inequality regions and forms a leaf shaped region. The minima now has to shift a bit to the left in order to satisfy all the constraints.
References
- Schulman, J., Duan, Y., Ho, J., Lee, A., Awwal, I., Bradlow, H., … & Abbeel, P. (2014). Motion planning with sequential convex optimization and convex collision checking. The International Journal of Robotics Research, 33(9), 1251-1270. [Link]